概率中的一些概念

Quantitative › 统计学
, , ,

一、概率、期望值、方差

  1. Random variable随机变量：风险资产的收益率是一个随机变量
  2. Outcomes结果：一个量，可能出现的结果
  3. Event事件：一组具体的实验结果
  4. Relationship among events
    1. Mutually exclusive events互斥事件: The events competing directly with each other that they would not happen at the same time.
    2. Exhaustive events 穷举事件：Events cover all possible outcomes.
    3. Independent events: A不依赖与B
    4. Dependent events: A的发生依赖与B
  5. 概率的定义：
    1. 任何事件E的概率是一个介于0-1之间的实数，即：0<= P(E) <=1
    2. 任何一个两两互斥切穷举的事件之和的概率为1
  6. 概率的类型
    1. Emprical probability 经验概率：根据历史数据所获得的相对发生频数作为事件发生概率的估计值
    2. Priori probability 先验概率：对于问题的逻辑推断所推导出来的概率
    3. Subjective probability 主观概率：一种基于个人或者主观判断而获得的概率
  7. Odds 胜率
    1. Odds for event E：P(E) / [1-P(E)], given a probability P(E)
    2. Odds against event E: [1-P(E)]/P(E)
  8. 无条件概率和条件概率
    1. Unconditional probability: P(A)
    2. Conditional probability: P(A|B)
  9. 联合概率和概率的乘法原则 Joint probability and multiplication rule
    1. Joint probability 联合概率：事件A和事件B同时发生的概率，被称作P(AB)
    2. Multiplication rule for joint probability 概率乘法法则：
      1. P(AB) = P（A|B）P（B）
      2. For independent rules：
        1. P(A|B) = P(A)
        2. P(AB) = P(A)P(B)
  10. 概率的加法原则 addition rule for probabilities
    1. P(A+B) = P(A) + P(B) - P(AB)
    2. 如果事件A和事件B是mutually exclusive，那么P(A+B) = P(A) + P(B)
  11. 全概率公式 Total probability rule：我们通常用全概率公式来分析事件发生的可能性。
    1. 公式：
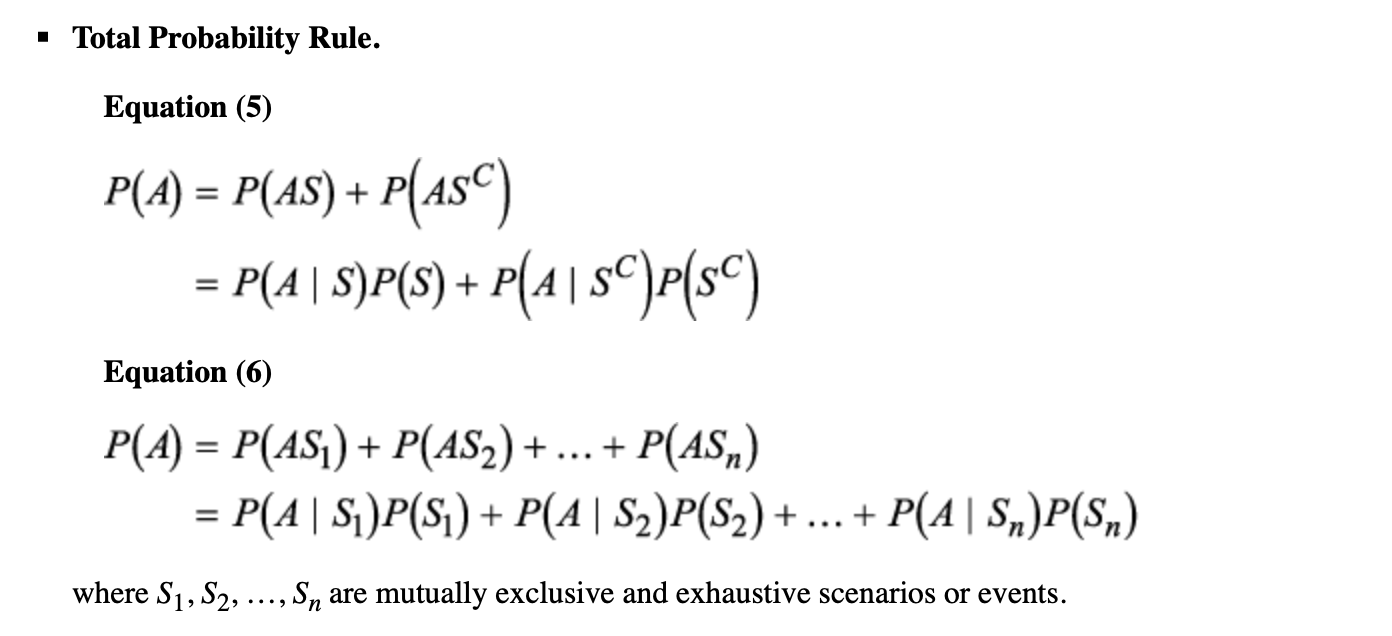
      total-probability-rule
    2. 示例：
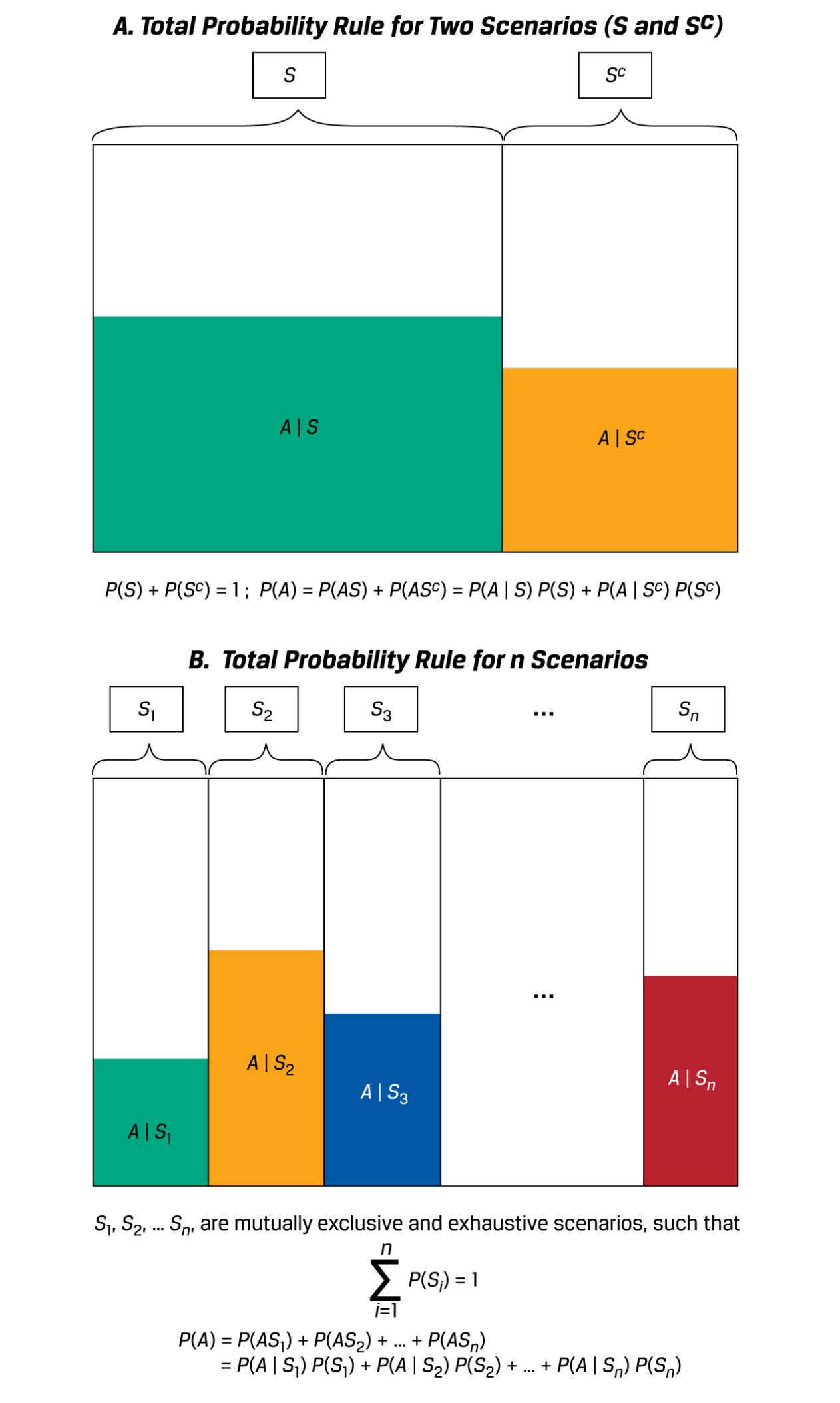
      total-probability-rule-scenarios
  12. 贝叶斯公式
    1. 定义：给定一组所关心事件的先验概率，如果你收到新的信息，那么更新你对于事件发生概率的法则。
    2. 公式：
      bayes-formula

二、投资组合的期望收益和期望方差

  1. 期望值的性质：

    1. 一个常数乘以一个随机变量的期望值等于该常数乘以该随机变量的期望值；
    2. 随机变量加权之和等于每个随机变量期望值相应权重的加权之和；

  2. Calculation of Portfolio Expected Return 投资组合收益率的计算方法

    1. 公式：
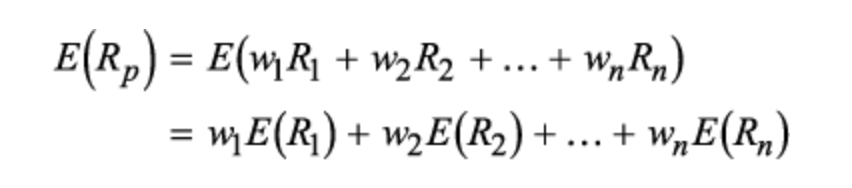
      Calc-portfolio-expected-return

  3. 方差：

    1. 公式： （）   （）

  4. 一个关于计算投资收益期望和方差的具体的例子

    Economy P(Xi) Return (Xi) P(Xi)Xi
    Recession 0.25 -0.10 -0.025
    Noraml 0.50 0.08 0.040
    Boom 0.25 0.22 0.055

根据期望收益公式：E（X） = -0.025 + 0.040 + 0.055 = 0.07

根据方差收益公式：Var(X) = 0.025*(-0.1-0.07)^2 + 0.5(0.08-0.07)^2 + 0.25(0.22-0.07)^2 = 0.01290

  1. 协方差 Covariance

    1. 定义：A measure to how two variables move together.
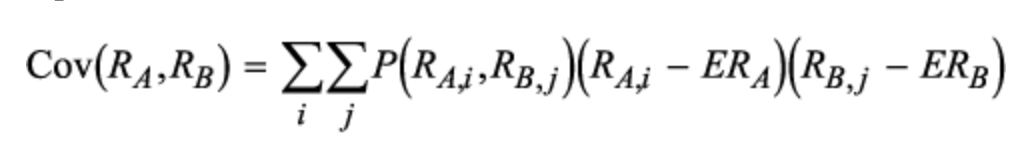
    2. 公式：cov-Ra-Rb

  2. 相关系数 Correlation

    1. 定义：A standardized measure of linear relationship between two variables.
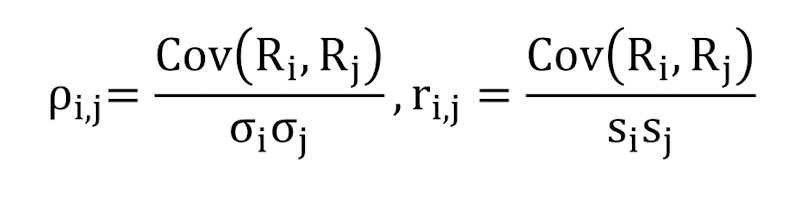
    2. 公式：correlation

  3. 协方差的计算

    1. 根据权重分别计算出A和B的期望收益；
    2. 根据协方差的公式在计算出协方差的值；

三、计数原理

  1. Labeling 标签问题：
    1. 定义：给n个元素标上k种不同的标签，第一类有n1个，第2类有n2个，以此类推n1+n2+nk，其分配的种类为：
    2. 公式：
  2. Combination 组合公式：
    1. 定义：当从列出的n(10)个元素中选出r(5)个元素的种类为：
    2. 公式：
    3. 金融计算器的计算方式：[10][2nd][+][5] = 252
  3. Permutation 排列公式：
    1. 定义：当从列出的n(10)个元素中选出r(5)个元素的种类，而且要考虑排列顺序：
    2. 公式：
    3. 金融计算器的计算方式：[10][2nd][-][5] = 30240