假设检验

大可

2023-11-21

Quantitative › 统计学

假设检验

Estimation： Addresses the questions such as “what is this parameter’s value”. 主要用于估计总体参数的值。
Hypothesis test：Addresses the questions such as “is the value of the parameter equal to a specific value”. 主要用于判断总体参数的某种假设是否成立。

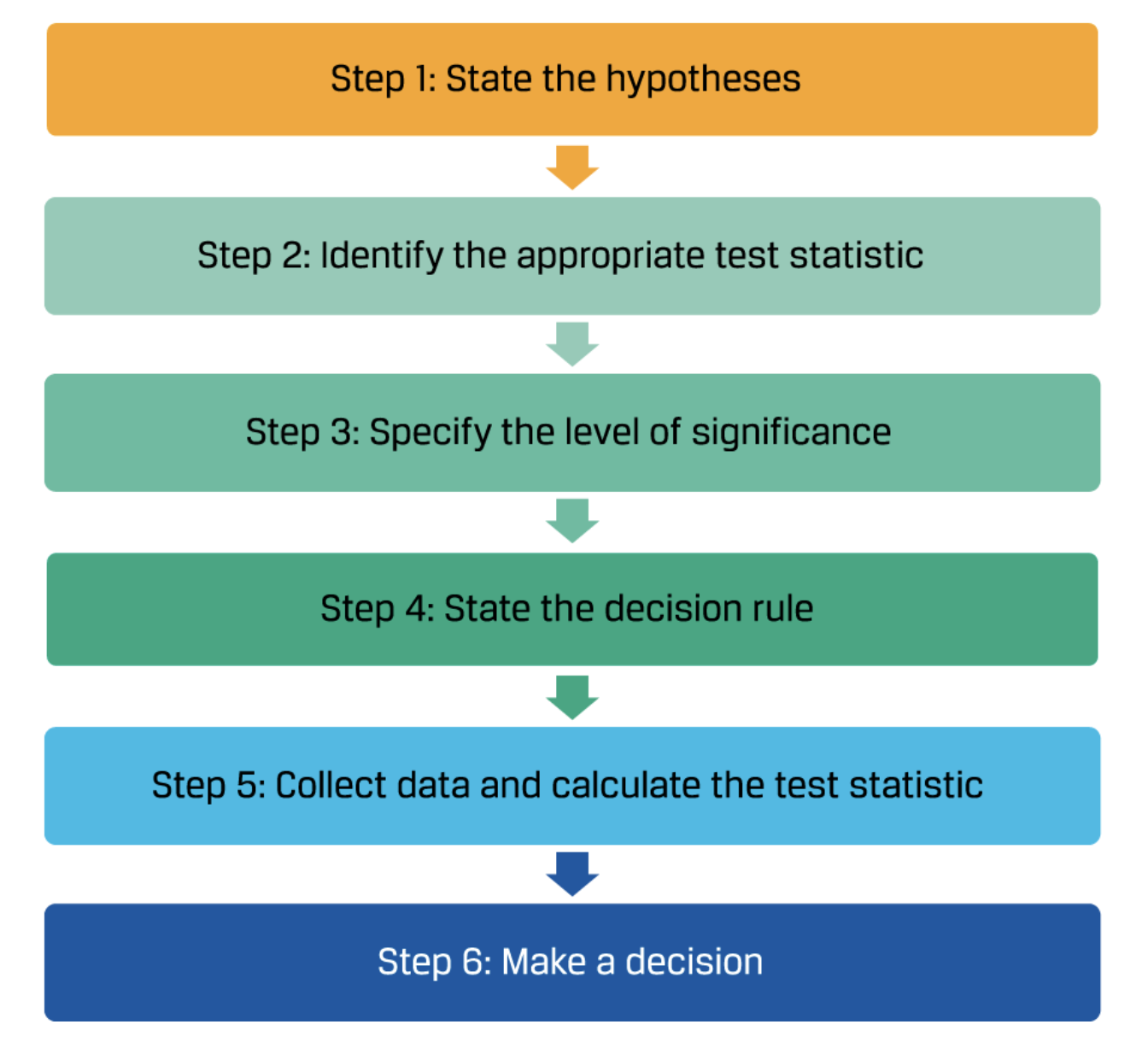
1. Stating the Hypotheses 给出假设

Null hypothesis vs. Alternative hypothesis
Null hypothesis 原假设:
1. 定义：Hypothesis to be tested. 例如一支股票每个月的回报率等于1%。
2. The “=” sigh will be only shown in null hypothesis. 只要带上等号，那么就是空假设。
3. 空假设一般是分析师想去拒绝的；
Alternative hypothesis 备择假设
1. The opposite side of null hypothesis.
2. 备择假设一般是分析师想去证明或者推断的。
3. 如果原假设被拒绝，那么备择假设就被接受或者证明。
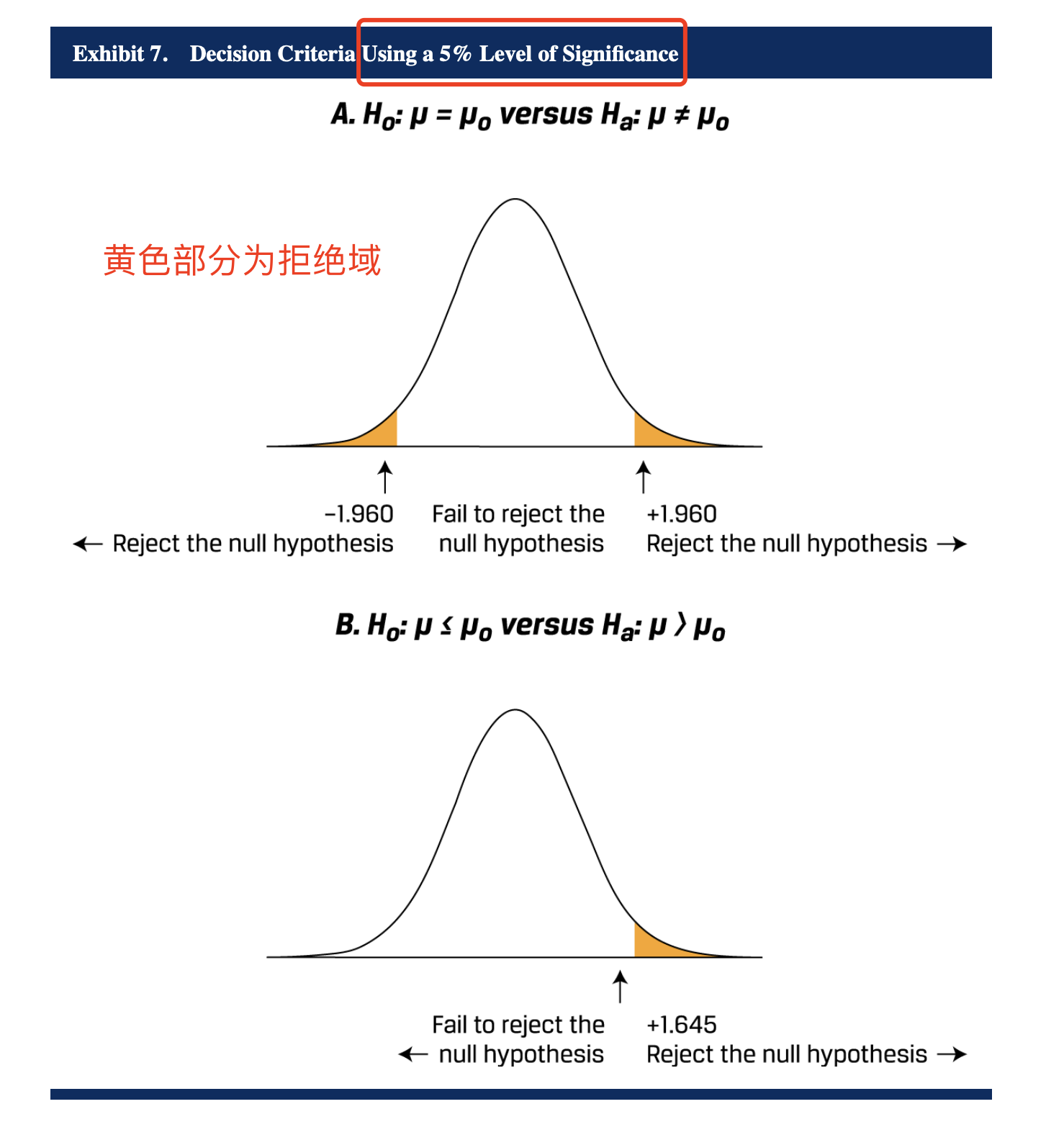
Two-tailed test 双尾检验
1. 我们想去检验一个population的均值是否等于6%；
One-tailed test 单尾检验
1. 我们想去检验一个population的均值是否大于6%

2. Identify the Appropriate Test Statistic 确定合适的检验统计量

3. Specify the level of significance 指定显著性水平

Significance level(σ) : 在假设检验中一类错误的概率记为希腊字母σ，这个概率被称为显著性水平。检验的一个0.05的显著性水平表示有5%的概率拒绝一个错误的原假设。
confidence level (1-σ).
“For example, a level of significance of 5% for a test means that there is a 5% probability of rejecting a true null hypothesis and corresponds to the 95% confidence level.”
我们在检验一个原假设时，有4种可能得结果：
1. 拒绝一个错误的原假设，这是一个正确的决策；
2. 我们拒绝一个正确的原假设，这被称为一类错误（type I error）；
3. 我们不能拒绝一个错误的原假设，这被称为二类错误（type II error）；
4. 我们不能拒绝一个正确的原假设，这是一个正确的决策；
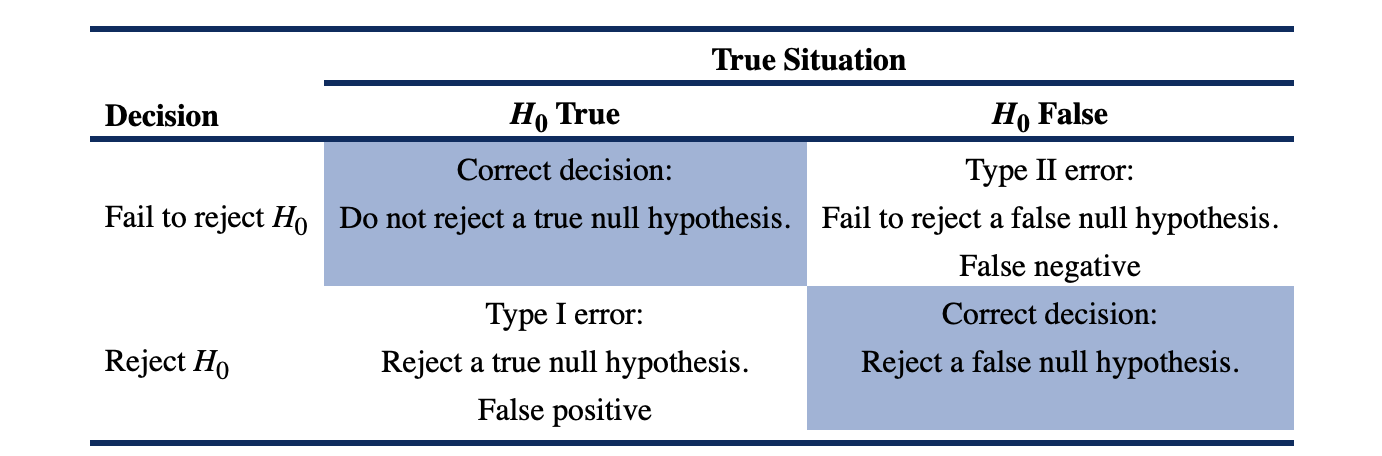
power of a test 检验的势: 正确拒绝原假设的概率，即在原假设为假时拒绝它的概率。
我们经常用来进行假设检验显著性水平有3个，分别为：0.10、0.05和0.01。如果我们在0.10的显著性水平拒绝了原假设，那么我们就具有了原假设为假的一些证据。如果我们在0.05的显著性水平下拒绝了原假设，那么我们就有了原假设为假的比较强的证据。如果我们在0.01的显著性水平下拒绝了原假设，那么我们就有原假设为假的相当强的证据。

4. State the decision rule 决策规则

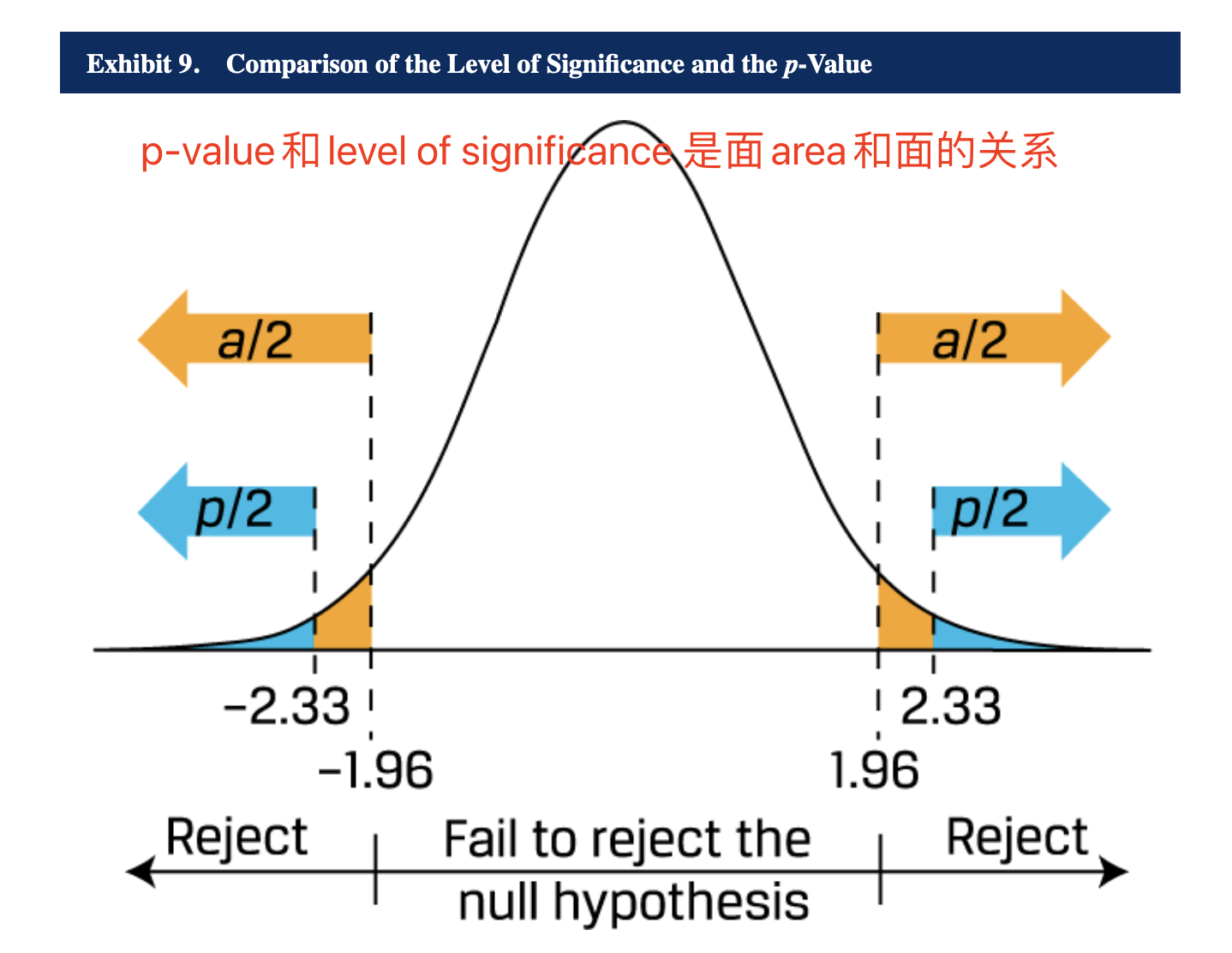
检验统计量的拒绝点（rejection point）(临界值（critical value）的定义)：一个检验统计量计算的拒绝点事与计算出来的检验统计量做比较的，以判断是否拒绝原假设的值；Rejection point是在显著性水平下的临界值。在双侧检验中，通常有两个拒绝点，分别位于分布的两端，使得拒绝域的总面积等于显著性水平（0.05）。
P-value：the area in the probability distributions outside the calculated test statistic.The smallest level of significance at which the null hypothesis can be rejected. p-value 是一个概率值，表示观察到的统计量或更极端情况发生的概率，用于直接比较显著性水平。
Decision rule
p-value和level-of-confidence的区别

5. Collect data and calculate the test statistic

6. Make a decision

统计学上的显著性并不能代表经济学上的显著性，因为在实践中有交易成本、税、风险。

Multiple tests（多重检验）：是指在同一组数据集上进行多次假设检验的情况。在进行多重检验时，需要考虑到累积的错误率，以避免由于进行多次检验而增加犯错误的概率。在多重检验中，常见的问题是“多重比较问题”或“多重假设问题”，其中对同一组数据进行多次比较可能导致弃真错误（Type I Error）的概率增加。为了控制整体的错误率，通常采用一些校正方法，如Bonferroni校正、Holm校正等。